Résistance au pivotement

La résistance au pivotement désigne l'ensemble des phénomènes qui s'opposent au mouvement de rotation d'une pièce autour d'un axe (ou arbre). Il est différent de la résistance au roulement qui concerne le mouvement d'une roue par rapport à son support. Le couple de freinage, ou encore le couple maximum transmissible d'un embrayage ou d'un limiteur de couple sont des cas particuliers de résistance au pivotement.

Les phénomènes physiques en œuvre sont :

• dans le cas d'un palier lisse, d'un frein ou d'un embrayage à friction : l'adhérence et le frottement (à l'instar de la résistance au glissement) ;
• dans le cas d'un palier à roulement : la résistance au roulement des éléments roulants (billes, rouleaux, aiguilles).

Si d'un point de vue microscopique, les phénomènes sont différents, en revanche, d'un point de vue macroscopique, ils sont pris en compte de la même manière, par un coefficient d'adhérence ou de frottement noté μ ou ƒ, ou bien par un angle d'adhérence ou de frottement φ (μ = tan φ).

Approche macroscopique

Couple moteur et couple résistant.

D'un point de vue macroscopique, la résistance au pivotement se caractérise par un couple résistant.

Considérons un système tournant, auquel on applique un couple moteur de moment M. En dessous d'une valeur seuil C_R, les phénomènes résistants créent un couple s'opposant exactement au couple moteur ; le système reste immobile (s'il s'agit d'un démarrage) ou bien ralentit (s'il s'agit d'un système déjà en mouvement). Au-delà de cette valeur, le couple résistant garde une valeur constante égale à C_R (ou légèrement inférieure), donc l'accélération angulaire ${\dot {\omega }}$ est dans le sens du mouvement. Toutefois, les phénomènes de frottement fluide augmentent avec la vitesse, le couple résistant peut donc croître avec la vitesse.

Selon le système étudié, la relation entre la charge appliquée au système et le couple résistant limite C_R s'exprime différemment.

Frottement tangentiel

Frein à sabot ou à tambour

Principe du frein à sabot.

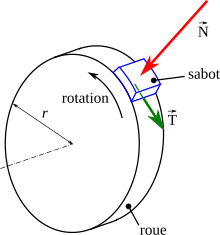
Les freins à sabot ou à tambour constituent un contact frottant sur une circonférence. Il peut s'agir :

• de la circonférence de l'arbre ;
• de la circonférence extérieure de la roue pour les freins à sabot (chariots à cheval, trains) ;
• de la circonférence intérieure de la roue pour les freins à tambour.

• Différents types de freins
• 
  Frein de chariot
• 
  Frein à sabot sur l'arbre d'une machine
• 
  Frein de train
• 
  frein à tambour à mâchoire intérieure

Considérons un petit élément de la surface de contact, suffisamment petit pour que l'on puisse considérer qu'il est plan. La force normale dN est une force radiale, le frottement résultant dT est une force tangentielle, et l'on a :

dT = μdN.

Cette force tangentielle crée un moment par rapport à l'axe de rotation valant

dM = R⋅dT,

R étant le rayon de la surface de contact.

Si l'effort normal se répartit de manière uniforme, ce qui est le cas si le sabot couvre un angle faible, on obtient donc le moment de résistance au roulement :

C_R = R⋅μ⋅N

N étant l'effort presseur.

Frein à tambour intérieur, desserré (gauche) et serré (droite).
1. Tambour. 2. Piston. 3. Ressort de rappel. 4. Garniture. 5. Mâchoire. 6. Pivot.

Représentation de la pression de contact garniture/tambour.

Dans le cas d'un frein à tambour à mâchoire intérieure (frein de tambour de voiture) ou extérieur, on considère que la pression de contact varie selon le sinus de l'angle polaire θ (θ = 0 pour le pivot du sabot) :

p = p₀⋅sin θ.

En intégrant, on a un couple résistant valant :

C_R = μ⋅p₀⋅b⋅r²(cos θ₁ - cos θ₂)

où

• b est la largeur de la mâchoire ;
• θ₁ et θ₂ sont les limites de la mâchoire.

Dans le cas d'un frein à sabot, supposé symétrique par rapport à l'articulation (θ₂ = -θ₁), on a

p = p₀⋅cos θ

et

C_R = 2⋅μ⋅p₀⋅b⋅r²sin θ₁

Palier lisse

Palier soumis à une charge radiale (le jeu est représenté de manière amplifiée).

Détermination du bras de levier et tracé du petit cercle.

Considérons un arbre soumis à une charge radiale F₁ dans un palier lisse ; le contact est cylindrique (liaison pivot glissant). L'action du palier est F₂. L'arbre subit également un couple moteur de moment M.

Au départ, il y a adhérence ; l'arbre « roule » dans le palier et « monte la côte ». Les forces F₁ et F₂ ne sont plus colinéaires mais sont sur deux axes parallèles, distants d'une distance d ; comme nous sommes à l'équilibre, on a

M = F₁⋅d = F₂⋅d.

Comme le profil est circulaire, la pente augmente. Pour une valeur donnée de M, l'angle vaut donc φ, l'angle limite d'adhérence ; l'arbre se met à glisser dans le palier, et donc à pivoter.

À ce point, l'action du palier est donc sur le cône d'adhérence. L'axe de ce cône est perpendiculaire à la surface en ce point, c'est donc un rayon, il passe par le centre de l'arbre. On voit que le cône s'appuie sur un cercle de rayon r valant :

r = d = R⋅sin φ.

Le couple résistant vaut donc

C_R = F₁⋅R⋅sin φ

Si la valeur de l'adhérence est faible, on a alors

sin φ ≃ φ

et

φ ≃ tan φ = μ

(φ en radians), donc

C_R ≃ F₁⋅R⋅μ ;

r ≃ R⋅μ.

Le tracé du petit cercle de rayon r permet une résolution graphique des problèmes.

Voir aussi

Bibliographie

 : document utilisé comme source pour la rédaction de cet article.

• [Fan2007] Jean-Louis Fanchon, Guide de mécanique : Sciences et technologies industrielles, Nathan, 2007, 543 p. (ISBN 978-2-09-178965-1), p. 83-86
• [Fan2011] Jean-Louis Fanchon, Guide des sciences et technologies industrielles : dessin industriel et graphes, matériaux, éléments de construction ou de machines..., La Plaine-Saint-Denis/Paris, AFNOR/Nathan, 2011, 623 p. (ISBN 978-2-12-494183-4 et 978-2-09-161590-5), p. 399-405
• [SG2003] D. Spenlé et R. Gourhant, Guide du calcul en mécanique : Maîtriser la performance des systèmes industriels, Hachette Technique, 2003 (ISBN 978-2-01-168835-4), p. 104-105